View on GitHub

essay

All about my technical essays and practicals

筹码，下注与资金管理

这篇文章主要讨论下注策略，也即所谓的资金管理。

在”从威尼斯人的赌桌到宽基ETF”中，交易过程被当作赌博的过程。每一次下注是否可以盈利是未知的，所以只能选取期望为正的赌局，不断下注，最终获利。但凡事皆有意外，很有可能因为极端情况的出现，导致多次交易后依然亏损。所以风险控制是成功交易系统必须考虑的部分。 为了控制风险，在每次交易前必须计算好下注的筹码大小，以实现风险控制。下注的策略有很多种，比如许多文章里面经常建议业余投资者的基金定投，就是一种常见的下注策略。

下注策略

在交易系统里，所谓下注策略，是指针对每次交易，分配不同的资金，以期保住盈利，实现收益最大化的策略。 在这里，下注策略有两层意义：

  1. 在一个正期望的交易系统里，交易者可以利用下注策略控制风险，实现盈利。下注策略无法使交易者在负盈利期望的交易中获利。因此在赌场中，赌徒是无法通过优化下注策略获胜的。
  2. 下注策略是资金管理的手段，它针对每次交易分配不同的资金，利用大数定律，实现目标收益最大化。因此利用下注策略无法实现在极端条件下的盈利。 多年以来，数学家，交易员，赌徒对下注策略进行了深入的研究。常见的策略有：
    • 马丁格尔（鞅策略）
    • 定投策略
    • 凯利公式 接下来我将结合随机游走的时间序列模型，来介绍和比较这些有名的下注策略。

      随机游走模型

      人们普遍认为每日收盘价格的变动是一个符合高斯分布的随机过程。比如选取601939从2017年7月到2019年7月的走势。 可以发现每日价格变动是一个典型的高斯分布

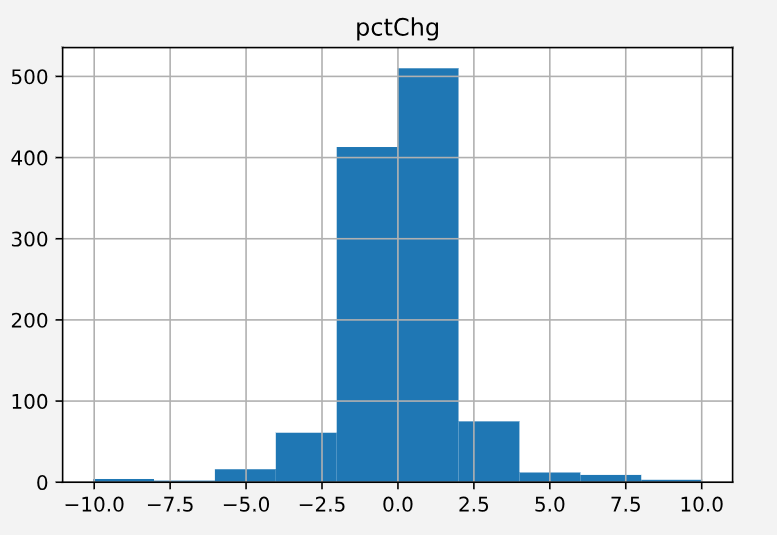
每日价格变动百分比

其均值为 0.043% 标准差 1.80%。所以接下来我用同样的特征模拟出一系列相似的随机过程。

import numpy as np 
import pandas as pd 
days = 250# 250个交易日
ss = pd.DataFrame() 
# 50个样本
for i in range(50): 
    value = [] 
    # 初始价格为1
    last = 1  
    # 均值0.05，标准差1.8的高斯分布
    change = np.random.normal(0.05, 1.8, days) 

    for idx, ch in enumerate(change): 
        value.append(last) 
        last = last * (100+ch) / 100  
    ss['ch'+str(i)] = value 

# 打印出所有样本的走势
ax = ss.plot.line()
ax.legend().remove()

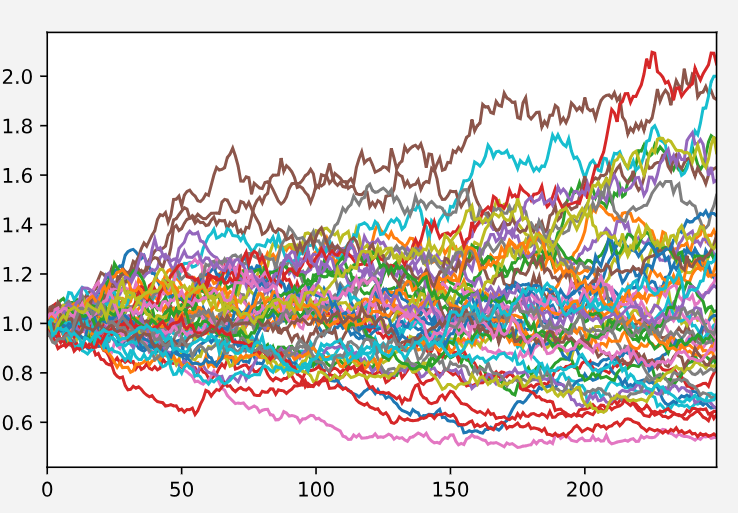
生成的每日收盘价格

价格变动直方图

利用这些模型，接下来将开始对上述提到的下注策略进行模拟。

马丁格尔策略

Martingale，也叫鞅策略，风靡于18世纪的法国。该策略非常简单，它基于这样一种假设：

亏损不可能一直发生，连续亏损越多次，下一次盈利的可能性就越大。因此每次亏损都翻倍下注，就可以在下次把钱全部赢回。

假设一个人初次投注为1，输了，那么下一次下注就是2，再下一次就是4，不断继续，直到用光所有筹码。显然，下注增加的速度是惊人的指数增长。即使首次下注只用1%的本金，那么连续输6次就会用光所有本金。 为了模拟这种下注策略，我们设定一旦用光所有本金，则持仓不动到结束。而一旦获利，则把下注金额重新定为1% 具体步骤如下：

  1. 设置一个单位为本金8%，首次下注一个单位
  2. 价格变动3个标准差则代表一次交易
  3. 输了翻倍追加本金，赢了将持仓调整为初始的一个单位
  4. 用光本金则一直持仓，直到盈利，重新开始

模拟代码如下：

# 价格变动的阈值
chg = 1.8 / 100 * 3
# 初始下注比例
ratio = 0.08
# 记录结果
result = []
# 基准收益
natural = []

def buy(price, bet):
    return bet / price

def sell(price, share):
    return price * share

ret = pd.DataFrame()

for sit in ss.columns:
    close = ss[sit]
    # 记录每日账户的总市值
    value_every = []
    cash = 100
    bet = 0
    share = 0
    buy_in_price = 0
    for price in close:
        value_every.append(cash+sell(price, share))
        if buy_in_price == 0:
            bet = ratio * cash
            buy_in_price = price
            share = buy(price, bet)
            cash -= bet
        
        # 盈利，卖出，重新买入一份
        if (price - buy_in_price)/buy_in_price >= chg:
            # sell out
            cash += sell(price, share)
            share = 0

            # buy inital unit
            bet = ratio * cash
            buy_in_price = price
            share = buy(price, bet)
            cash -= bet

        # 亏损，翻倍下注
        if (buy_in_price - price)/buy_in_price >= chg:
            # doubel bet or all in
            if cash >= bet*2:
                bet = bet * 2
                buy_in_price = price
                share += buy(price, bet)
                cash -= bet
            elif cash > 0:
                bet = cash
                buy_in_price = price
                share += buy(price, bet)
                cash -= bet
    
    total_value = cash + sell(close.iloc[-1], share)
    result.append(total_value)
    natural.append(close.iloc[-1]*100)
    
    ret[sit] = value_every

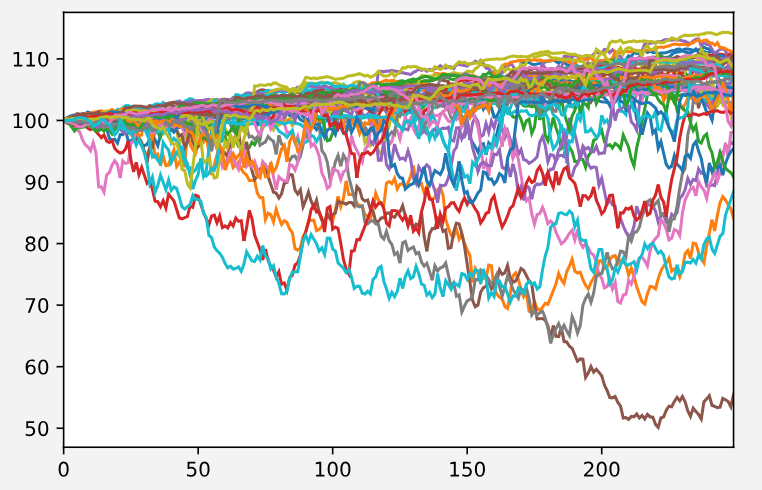各个模型对应的收益曲线 在好的行情里该策略远远跑输基准，而在很糟糕的行情里也并不能减少损失。从这两点看来，马丁格尔策略并不是一个好的下注策略。不过值得一提的是，在后续的箱型图对比中可以发现，该策略中位数较高，而标准差很小，大部分情况下都不会有很大的亏损。因此，如果遇上平淡无味的行情时，比如长期震荡的行情，该策略或许值得一试。

定投

很多文章推荐小白采用定投策略：每隔一段时间或者价格变动超过一定幅度，就投入相同比例的资金。这些文章都用过去几年沪深300的情况来举例，说明定投的优点。但这个策略实际如何呢？ 为了模拟该策略在不同模型下的情况，有下述模拟步骤：

  1. 设置一个单位为本金25%，每次下注一个单位
  2. 价格变动3个标准差则代表一次交易
  3. 当发现没有本金时，则卖出所有，并开始新一轮定投 ```python ratio = 0.25 result = [] ret = pd.DataFrame()

for sit in ss.columns: value_every = [] close = ss[sit] cash = 100 bet = ratio * cash share = 0 buy_in_price = 0 for price in close: value_every.append(cash+sell(price, share))

    if buy_in_price == 0:
        buy_in_price = price
        share = buy(price, bet)
        cash -= bet
    
    if abs(price - buy_in_price)/buy_in_price >= chg:
        if cash == 0:
            # sell out
            cash += sell(price, share)
            share = 0

        bet = ratio * cash
        if cash >= bet:
            buy_in_price = price
            share += buy(price, bet)
            cash -= bet
        
        elif cash > 0:
            buy_in_price = price
            share += buy(price, cash)
            cash -= cash


total_value = cash + sell(close.iloc[-1], share)

result.append(total_value)
ret[sit] = value_every ``` ![定投策略](https://images.xiaozhuanlan.com/photo/2019/3a5266a1bd7ada68a73f1829f21488dc.png) 该策略在大部分行情下的收益曲线与基准相差不大，收益曲线变动曲线稍微变窄，而且极端情况下的表现不算太糟。总的来说是一个不错的策略。 ## 凯利公式 将每次交易看成是一次赌博过程。止盈点为上涨b1，止损点为-b2，上涨概率p，则下跌概率1-p。那么期望收益的对数则为 `(1+fb1)log(p)+(1+fb2)log(1-p)=ret`，简单求导可知当`f = (p-1)/b1-p/b2`，期望收益取得最大。如果b2等于1，则退化经典的凯利公式。 即 `f = (p-1)/b - p`。一个非常有名的资金控制策略。 为了验证该公式，模拟步骤如下： 1. 假设价格上涨超过均值三个标准差和下跌超过均值3个标准差的概率相同 2. 一旦价格触及上述位置则代表一次交易 3. 用凯利公式计算每次下注大小 ```python def my_kelly(p:float, b1:float, b2:float):
return (p-1)/b1-p/b2 ratio = my_kelly(0.5, (0.05+1.8*3)/100, (0.05-1.8*3)/100) result = [] ret = pd.DataFrame() chg = 1.8 / 100 for sit in ss.columns:
value_every = []
close = ss[sit]
cash = 100
bet = ratio * cash
share = 0
buy_in_price = 0
for price in close:
    value_every.append(cash+sell(price, share))

    if buy_in_price == 0:
        buy_in_price = price
        share = buy(price, bet)
        cash -= bet
    
    if (price - buy_in_price)/buy_in_price >= (0.05+1.8*3)/100 or (price - buy_in_price)/buy_in_price <= (0.05-1.8*3)/100:
        if cash == 0:
        # sell out
            cash += sell(price, share)
            share = 0
            bet = ratio * cash
            if cash >= bet:
                buy_in_price = price
                share += buy(price, bet)
                cash -= bet


total_value = cash + sell(close.iloc[-1], share)
ret[sit] = value_every

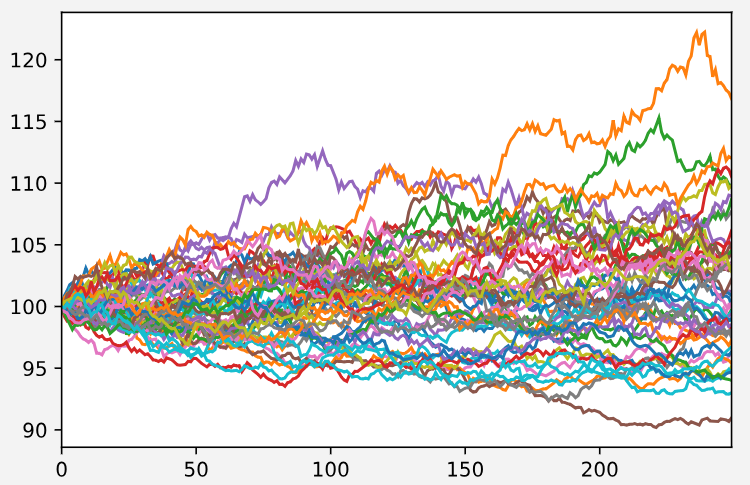``` kelly公式各个模型对应的收益曲线 结果看上去乏善可陈，虽然在很差的行情下亏损很少，但是遇上好的行情远远跑输基准。难道是理论错了么？并非如此。 凯利公式的应用需要事先知道每次交易的赔率和胜率，而上面假设的 价格上涨超过均值三个标准差和下跌超过均值3个标准差的概率相同 并不准确，所以凯利公式计算出来的比例是失真的。如果把条件改为 价格上涨超过均值1个标准差和下跌超过均值1个标准差的概率相同， 计算出来的比例是1.5。即凯利公式认为这种情况应该1.5倍杠杆下注。这种情况下模拟出来的收益曲线是：

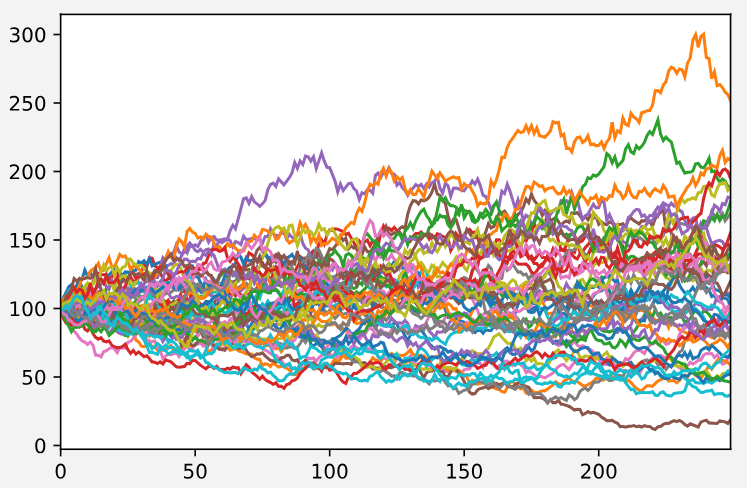
leverage

最高收益300%，而最惨的情况是爆仓，即亏掉全部本金，期望收益16%，是all in的两倍，果然高风险还是值得的。

这个例子说明，应用凯利公式的关键是选取正确的赔率和胜率，而且凯利公式计算出来的值有时会建议加杠杆。由于该公式没考虑到杠杆成本，所以实际上不能简单照搬使用。

总结

上述策略模拟结果的箱型图如下。natural列是基准收益，各自的期望收益是 8%， 4%， 7% 和 2%。马丁格尔策略的标准差是最小的，但是无法抵御极端情况。定投对极端情况有一定抵御作用，但不太明显。而凯利公式由于设计赔率和胜率的选取，模拟出来的结果不具代表性。对比这些策略的期望收益还可以发现，不考虑杠杆的情况下，all in的策略期望是最高的。这也是意料之中的，因为一开始的模型就是一个正期望的走势。

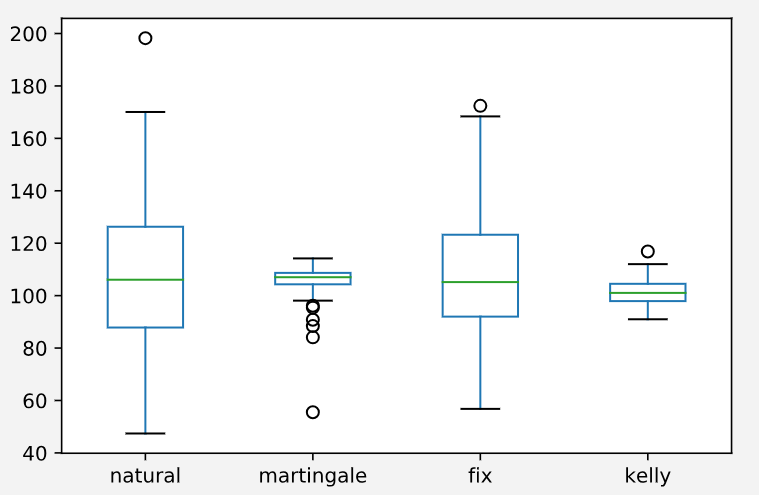
各个策略收益对比图

通过这些对比，还是说明了选股，或者选择交易标的才是最重要的。如果遇到了一个正期望的交易标的，其实all in的期望收益是最好的。如果只是单纯求稳，那么即使遇上很好的行情也无法获得可观盈利。

一句话，选择赛道才是盈利的核心。